آزمون ریاضی گاج ___ پایه هفتم

---

امتحان ریاضی ____ پایه هفتم ____ کل کتاب + جواب

این آزمون به صورت عکس است. 

---

---

---

---

---

---

 

آزمون ریاضی فصل پنجم شمارنده ها و اعداد اول

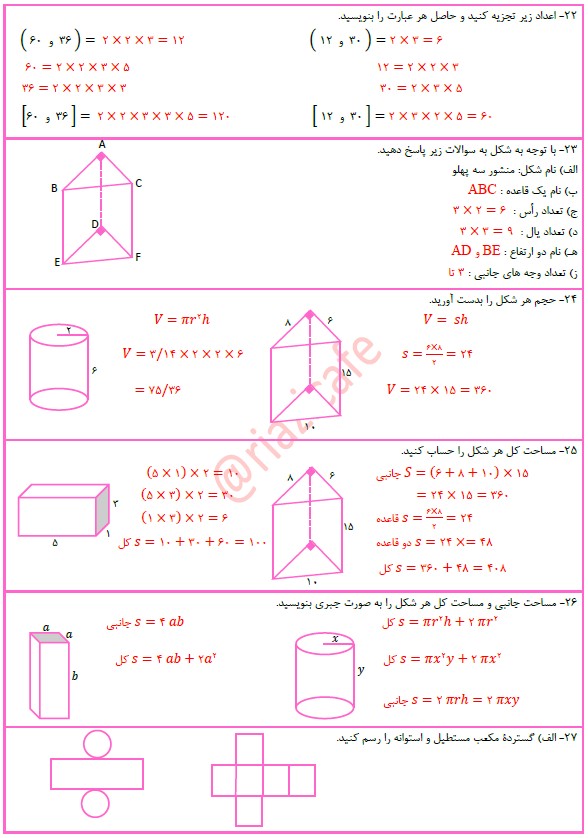
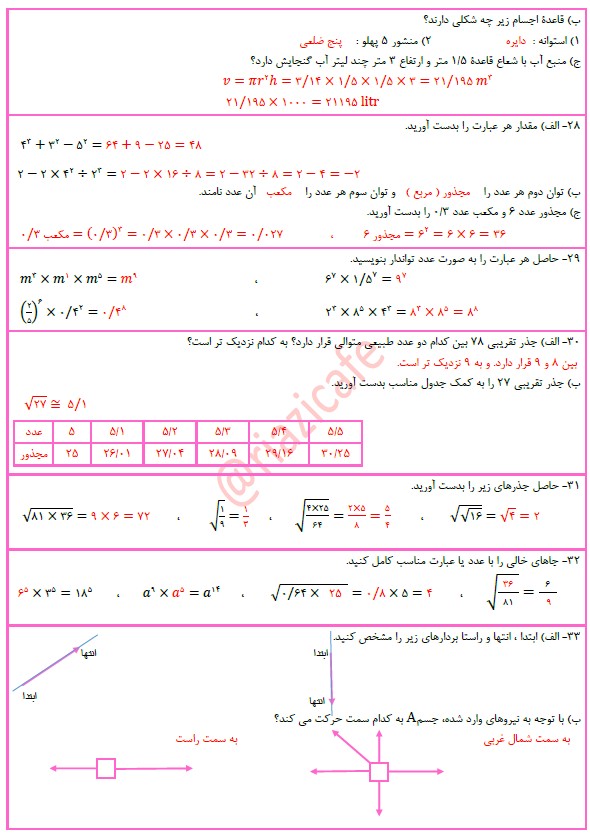
1- درستی یا نادرستی جملات زیر را مشخص کنید

الف ( کوچکترین شمارنده هر عدد ، خود عدد است
ب ( اگر دو عدد بر هم بخشپذیر باشند ، ک.م.م آنها عدد کوچکتر است.
ج ( همه اعداد اول فرد هستند .
د ( عددی که یک شمارنده اول داشته باشد، عددی اول است.

2- از بین جواب های داده شده ، پاسخ صحیح را انتخاب کنید و در جای خالی بنویسید

الف ( کوچکترین مضرب مشترک دو عدد اول ، ................................... است. ( عدد یک حاصل ضرب آنها ) –
ب ( عدد 63 دارای .......................... شمارنده اول است. (دو تا چهار تا) -
ج ( عدد ........................ بر همه اعداد بخشپذیر است. ( عدد یک عدد صفر ) -
د ( اگر a عددی اول باشد، دارای ............................. مضرب اول است . (یک هیچ )

3-تمام شمارنده های عدد های 85 و 80 را بنویسید و بزرگترین شمارنده مشترک آنها را مشخص کنید.

 

 

4-عددهای اول بین 20 تا 40 را بنوسید.

 

 

5-با استفاده از تجزیه اعداد تساوی های زیر را کامل کنید.

(54, 24)=
[54, 24]=

6-با استفاده از نمودار درختی عدد های زیر را تجزیه کنید و سپس به صورت حاصلضرب شمارنده های اول بنویسید.

98=                                                                   40=

7-میخواهیم یک زمین مستطیلی شکل به ابعاد 60 و 210 سانتی متر را فقط با موزاییک های مربعی شکل بپوشانیم.
الف ( بزرگترین مقدار ممکن برای طول ضلع هر موزاییک چقدر است ؟

 

ب ( حداقل تعداد موزاییک های لازم را حساب کنید.

مساحت و محیط اشکال هندسی

۱)مساحت مـــربع = یـــک ضلع × خـــودش
محیــط مـــربــــع = یک ضلع × ۴


::) مساحت مسـتطیـــــــل = طـول × عـرض
محیط مستطیل = ( طول + عرض) × ۲


۳) مساحت مثلث = ( قاعده × ارتــــــفاع ) ÷ ۲
محیط مثلث = مجموع سه ضلع


۴) مساحت مثلث متساوی الاضلاع = ( قاعده × ارتفاع ) ÷ ۲
محیط مثلث متساوی الاضلاع = یک ضلع × ۳


۵) مساحت مثلث متساوی الساقین = ( قاعده × ارتفاع ) ÷ ۲
محیط مثلث متساوی الساقین= مجموع سه ضلع


۶) مساحت مثلث قائم الزاویه = ( قاعده × ارتفاع ) ÷ ۲
محیط مثلث قائم الزاویه = مجموع سه ضلع


۷) مساحت ذوزنقه = ( قاعده بزرگ + قاعده کوچک ) × نصف ارتفاع
محیط ذوزنقه = مجموع چهار ضلع


۸) مساحت لوزی = ( قطر بزرگ × قطر کوچک ) ÷ ۲
محیط لوزی = یک ضلع × ۴


۹) مساحت متوازی الاضلاع = قاعده × ارتفاع
محیط متوازی الاضلاع = مجموع دو ضلع متوالی × ۲


۱۰) مساحت دایره = عدد پی ( ۱۴/۳ ) × شعاع × شعاع
محیط دایره = عدد پی ( ۱۴/۳ ) × قطر


۱۱) مساحت کره = ۴ × ۱۴/۳ × شعاع به توان دو

حجم کره = چهار سوم × ۱۴/۳ × شعاع به توان سه



۱۲) مساحت بیضی = (نصف قطر بزرگ × نصف قطر کوچک ) × ۱۴/۳


۱۳ ) محیط چند ضلعی منتظم = یک ضلع × تعداد اضلاعش


۱۴ ) حجم مکعب مستطیل = طـول × عـرض × ارتفاع
حجم مکعب مربع = قاعده × ارتفاع ( طول یال×مساحت یک وجه)


۱۵ ) حجم هرم = مساحت قاعده ی هرم × ارتفاع هرم× یک سوم


۱۶) مساحت جانبی استوانه = محیط قاعده × ارتفاع حجم استوانه = مساحت قاعده × ارتفاع

سطح کل استوانه = سطح دو قاعده + مساحت جانبی ( مساحت مجموع دو قاعده + ارتفاع × پیرامون قاعده )


۱۷) مساحت جانبی منشور = مجموع مساحت سطوح جانبی
مساحت کلی منشور = مجموع مساحت دو قاعده + مجموع مساحت سطوح جانبی


۱۸) حجم مخروط = مساحت قاعده × یک سوم × ارتفاع

جزوات ریاضی پایه ((هفتم))

دانلود جزوه فصل اول ریاضی پایه هفتم – (برای دانلود کلیک کنید)

دانلود جزوه فصل دوم ریاضی پایه هفتم – (برای دانلود کلیک کنید)

دانلود جزوه فصل سوم ریاضی پایه هفتم – (برای دانلود کلیک کنید)

دانلود جزوه فصل چهارم ریاضی پایه هفتم – (برای دانلود کلیک کنید)

دانلود جزوه فصل پنجم ریاضی پایه هفتم – (برای دانلود کلیک کنید)

دانلود جزوه فصل ششم ریاضی پایه هفتم – (برای دانلود کلیک کنید)

دانلود جزوه فصل هفتم ریاضی پایه هفتم – (برای دانلود کلیک کنید)

دانلود جزوه فصل هشتم ریاضی پایه هفتم – (برای دانلود کلیک کنید)

دانلود جزوه فصل نهم ریاضی پایه هفتم – (برای دانلود کلیک کنید)

متغیر : حروف انگلیسی که نشان دهنده ی عددی است که تغییر می کند.

ضریب : به عددی که کنار متغیر باشد و بین آن ها علامتی نباشد یا علامت ضرب باشد. ضریب می گویند.

یک جمله ای جبری : عبارت جبری که از دو قسمت عدد )ضریب( و متغیر تشکیل شده باشد. مانند 5𝑥𝑦:

چند جمله ای جبری : اگر بین عبارت های جبری علامت جمع و تفریق باشد تشکیل چند جمله ای میدهد.

عبارت جبری متشابه : عبارتی که متغیر های آن )حروف انگلیسی( کاملا شبیه هم باشند.
عبارت جبری نا متشابه : عبارتی که متغیرهای آن شبیه هم نباشند.
ساده کردن عبارت های جبری : جملات متشابه را جدا کرده سپس مانند جمع و تفریق اعداد صحیح آن ها را جواب داده با این تفاوت که حروف کنار اعداد نوشته می شود.

مثال : عبارت های جبری زیر را ساده کنید.

−4𝑥 + 2𝑦 + 13𝑥 = 6𝑥 + 2𝑦

ضرب عدد در عبارت جبری : اگر عددی قبل از پرانتز باشد و بین آن ها علامتی نباشد آن عدد در تمام جملات پرانتز ضرب می کنیم.

مثال : عبارت جبری زیر را ساده کنید.

2(3𝑎 − 2𝑏) − (𝑎 + 3𝑏) = 6𝑎 − 4𝑏 − 𝑎 − 3𝑏 = 5𝑎 − 7𝑏

مقدار عددی عبارت جبری : به جای حروف اعداد داده شده را قرار می دهیم سپس جواب می دهیم.

نکته : در محاسبه مقدار عددی اگر عبارت جبری قابل ساده شدن بود ابتدا عبارت را ساده سپس مقدار عددی را به دست می آوریم.

به دست آورید.𝑏 = و 3 𝑎 = − مثال : مقدار عددی عبارت زیر را به ازای 0

3(𝑎 − 2𝑏) + 2(−2𝑎 − 𝑏) = 3𝑎 − 6𝑏 − 4𝑎 − 2𝑏 = −𝑎 − 8𝑏 = −1(−2) − 8(3) = 2 − 24 = −22

معادله : معادله یک تساوی جبری است که به ازای بعضی از اعداد به یک تساوی درست تبدیل می شود.

نکته : هر معادله از سه قسمت تشکیل شده است : 1( ضریب )عدد کنار متغیر( 2( مجهول )متغیر( 3( معلوم )عدد بدون متغیر(

نکته : برای حل معادله مراحل زیر را به ترتیب انجام می دهیم :

1( مجهول ها را به طرف چپ و عددهای معلوم را به طرف راست انتقال می دهیم. )عددی که انتقال داده شود علامت آن عوض می شود(

2( عددهای مجهول با هم و عددهای معلوم را با هم جواب می دهیم.

3( حاصل عددهای معلوم را بر حاصل عددهای مجهول تقسیم می کنیم.

نکته : در معادلات کسری ابتدا مخرج را با استفاده از )ب.م.م( مخرج ها از بین می بریم سپس معادله را حل می کنیم. مانند :

ابتدا )ب.م.م( مخرج یعنی عدد 6 را در دو طرف معادله ضرب کرده تا با مخرج ساده و مخرج از بین برود :

 

 

عددهای صحیح فصل دوم درسنامه و نکات کلیدی

جمع اعداد صحیح : برای جمع اعداد صحیح از روش های زیر استفاده می کنیم :

الف( مختصر نویسی : دو عدد را با علامتشان بدون پرانتز کنار هم می نویسیم. اگر دو عدد هم علامت باشند دو عدد را جمع و اگرمختلف العلامت باشند دو عدد را کم می کنیم و برای جواب علامت عدد بزرگتر را قرار می دهیم.

 

ب( محور اعداد : با توجه به اعداد و علامت آن ها روی محور حرکت کرده انتهای حرکت دوم جواب حاصل جمع را نشان می دهد.

 

ج( دایره توپر و توخالی : برای عدد منفی دایره توپر و برای عدد مثبت دایره توخالی قرار داده و هر دایره توپر و توخالی همدیگر را خنثی می کنند. دایره های باقیمانده جواب حاصل جمع را نشان می دهد.

د( جدول ارزش مکانی : دو عدد را با توجه به ارزش مکانی آن ها در جدول قرار داده و گسترده هر عدد را کنار جدول نوشته و اعداد را ستونی جواب می دهیم.

تفریق اعداد صحیح : تفریق را به جمع تبدیل می کنیم. به این صورت که عدد اول را نوشته و عدد دوم را قرینه می کنیم.

حل مسئله اعداد صحیح : الف( اگر در مسئله ای دمای یک شهر را خواسته باشد بین دو عدد علامت جمع می گذاریم.
مثال : دمای شهر زاهدان 12 درجه بالای صفر و دمای سراوان 7 درجه سردتر از زاهدان است. دمای شهر سراوان چند درجه است؟

5+=(+12) + (−7)

ب( اگر در مسئله ای سردی یا گرمی هوا را خواسته باشد بین دو عدد علامت تفریق می گذاریم.
مثال : دمای مشهد 8 درجه بالای صفر و دمای اصفهان 6 درجه زیرصفر است. دمای اصفهان چند درجه سردتر از شیراز است؟

14-=(−6) − (+8) = (−6) + (−8)

ج( اگر در مسئله ای اختلاف دمای دو شهر را خواسته باشد بین دو عدد علامت تفریق می گذاریم.
مثال : دمای بیرجند 6 درجه زیر صفر و دمای بندر عباس 13 درجه بالای صفر است. اختلاف دمای دو شهر چند درجه است؟

(+13) − (−6) = (+13) + (+6) = +19

د( اگر در مسئله ای میانگین دمای دو شهر را خواسته باشد بین دو عدد علامت جمع قرار داده و در آخر جواب را بر تعداد اعداد تقسیم می کنیم.

مثال : حداکثر دمای هوای کرمان 18 درجه بالای صفر و حداقل دمای هوا 4 درجه بالای صفر است. میانگین دمای هوای این شهر چند درجه است؟

ضرب و تقسیم اعداد صحیح : در ضرب و تقسیم اعداد صحیح ابتدا ضرب علامت ها را انجام می دهیم سپس با توجه به علامت بین آن ها دو عدد را ضرب یا تقسیم می کنیم.

مثال : حاصل ضرب و تقسیم های زیر انجام دهید؟

(−12) × (+4) = −48                  (+24) ÷ (+8) = +3

 

 

آزمون آنلاین ریاضی فصل 6

اطلاعات تست

---

تعداد سوال:5

نمره ی هر سوال:20

نمره ی کل از 100 است

---

برای ورود به آزمون کلیک کنید.

---

 

نکته---->نام و نام خانوادگی و ایمیل خود را وارد کنید

 

نمونه سوال ریاضی فصل 1

نمونه سوال ریاضی همراه با جواب

---

نمونه سوال----->کلیک کنید

جواب نمونه سوال----->کلیک کنید

تست ریاضی پایه ((هفتم))

اطلاعات تست:

-----------------------------

تعداد سوال: 5

نمره  ی هر سوال: 20

نمره ی کل از 100 است

------------------------------------------

برای ورود کلیک کنید

-----------------------

نکته->لطفا اسم و فامیل و ایمیل خود را وارد کنید.